Nella disciplina del Project Management, il float (o slack) è la quantità di tempo che la data di inizio di un’attività di progetto può esser fatta ritardare, senza causare un ritardo alle attività successive (“Free Float“) o alla durata totale del progetto (“Total Float“).
Il concetto di Total Float è associato al cammino in un network diagram: se in un diagramma vi sono 4 cammini non critici, allora il progetto potrebbe avere 4 valori di Total float. Il Total float di un cammino è la combinazione dei valori del Free Float di tutte le attività del cammino.
Il Total Float di un’attività è calcolato come la differenza tra la Late Start e la Early Start (differenza tra la data di inizio massima e la data di inizio minima):
TF = LS – ES
In realtà può essere calcolato anche come la differenza tra la Late Finish e la Early Finish (differenza tra la data di fine massima e la data di fine minima):
TF = LF – EF
Il Free Float (detto anche Free Slack) è la quantità di tempo di cui può esser fatta ritardare la data di inizio di un’attività, senza che questo causi una variazione della data di inizio delle attività successive. Viene calcolato come la differenza tra la Late Finish di un’attività A e la Early Start dell’attività successiva B (differenza tra la data di fine massima di un’attività e la data di inizio minima della successiva):
FF = LFA-ESB
Il Project Management Body of Knowledge (PMBOK®) definisce il percorso critico come:
la sequenza delle attività presenti nel reticolologico di un progetto, che determina la durata del progetto
Si tratta quindi di quella sequenza di attività che determina la durata minima del progetto (di solito il cammino più lungo).
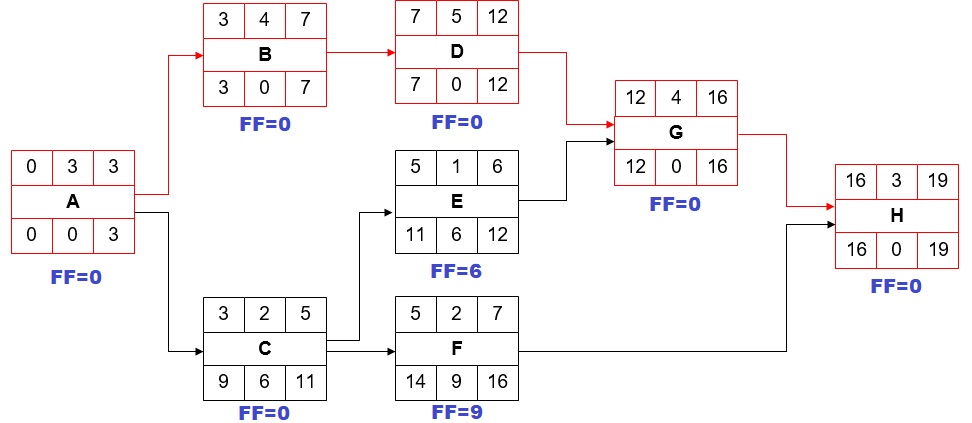
Vediamo un esempio di calcolo del Free Float e del percorso critico.
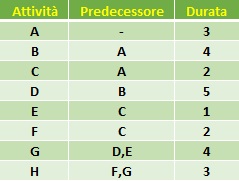
Supponiamo di avere la seguente tabella delle attività:
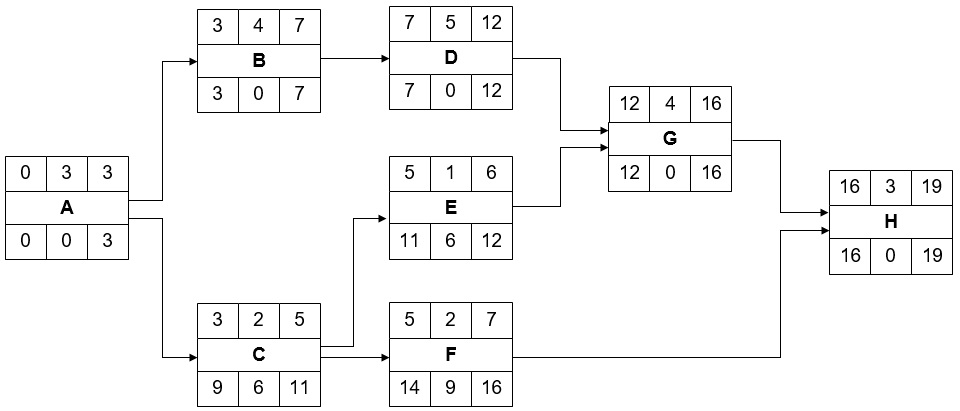
Questo ci porta al seguente diagramma reticolare (AON):
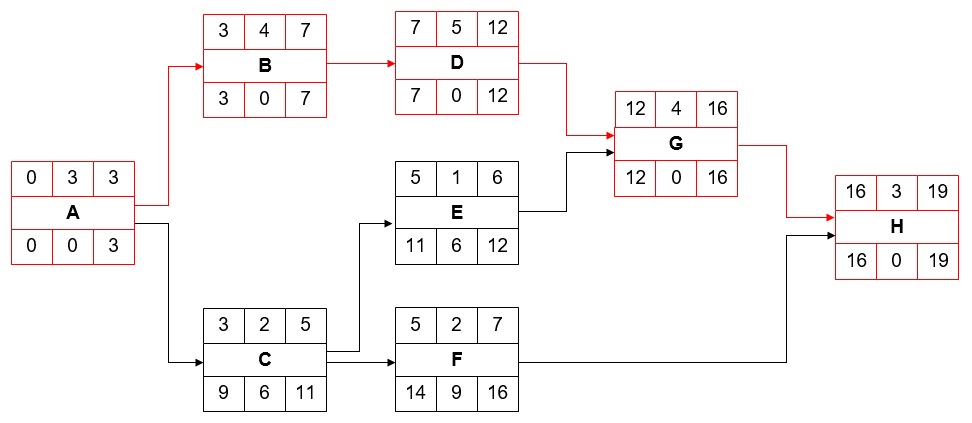
Mediante inspection, andando a prendere in considerazione i total Float delle attività, appare subito evidente che il percorso avente tutti i TF a 0 è il certamente percorso critico:
Ora calcoliamo il Free Float (FF), che per un’attività A è il minimo ES di tutte le attività successive, meno l’ES dell’attività stessa, meno la sua durata:
FFA = Min(ESB, ESC) – ESA – Durata(A)
Quindi nel caso nostro per l’attività A abbiamo:
FFA = Min(3, 3) – 0 – 3 = 0
Eseguendo lo stesso calcolo per tutte le attività, si ha:
Fonti:
- Wikipedia: Float (project management)
- YoutTube: What is Total Float (Total Slack) and how to calculate it in a network diagram
- YouTube: Determine Total Float & Free Float (AKA “Slack”) of activities in a network diagram
- PMBOK® Guide 6th Edition
Immagini:
- Public domain images from Pexels